Оценка моделей логистической регрессии

Этот вопрос возникает из-за моей путаницы в том, как решить, достаточно ли хороша логистическая модель. У меня есть модели, которые используют состояние пар индивидуальный проект через два года после их формирования в качестве зависимой переменной. Результат успешен (1) или нет (0). У меня есть независимые переменные, измеренные во время формирования пар. Моя цель - проверить, влияет ли переменная, которая, как я предположил, влияет на успех пары, на этот успех, контролируя другие потенциальные влияния. В моделях переменная интереса значительна.

Модели оценивались с использованием glm()функции в R. Чтобы оценить качество моделей, я сделал несколько вещей: glm()дает вам residual deviance, по AICи BICпо умолчанию. Кроме того, я рассчитал частоту появления ошибок в модели и составил график остатков.

Полная модель имеет меньшее остаточное отклонение, AIC и BIC, чем другие модели, которые я оценил (и которые вложены в полную модель), что заставляет меня думать, что эта модель «лучше», чем другие.
ИМХО (как в Gelman and Hill, 2007, pp.99 ): частота ошибок в модели достаточно низкая,
error.rate <- mean((predicted>0.5 & y==0) | (predicted<0.5 & y==1)около 20%.

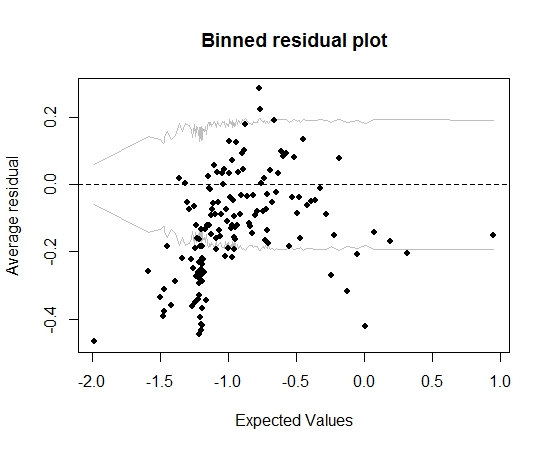
Все идет нормально. Но когда я строю график остатков (опять же по совету Гелмана и Хилла), большая часть контейнеров выходит за пределы 95% -ного КИ: Участок Binned Residuals

Этот сюжет заставляет меня думать, что в модели что-то совершенно не так. Должно ли это привести меня к выбрасыванию модели? Должен ли я признать, что модель несовершенна, но сохранить ее и интерпретировать влияние переменной интереса? Я поэкспериментировал с исключением переменных по очереди, а также с некоторым преобразованием, без реального улучшения графика с остатками.

Редактировать:

На данный момент модель имеет десяток предикторов и 5 эффектов взаимодействия.
Пары «относительно» независимы друг от друга в том смысле, что все они сформировались за короткий промежуток времени (но не строго говоря, все одновременно), и есть много проектов (13 тыс.) И много людей (19 тыс.). ), поэтому значительную часть проектов объединяет только одно лицо (около 20000 пар).

r logistic goodness-of-fit residuals Антуан Верне
источник

Y

$Y$

Исходя из того, что вы говорите, размер выборки не является проблемой, потому что у меня около 20000 тысяч пар (из которых примерно 20% успешны).

Антуан Вернет

Ответы:

Точность классификации (частота ошибок) - это неправильное правило оценки (оптимизированное фиктивной моделью), произвольное, прерывистое и простое в управлении. Это не нужно в этом контексте.

Вы не указали, сколько было предсказателей. Вместо того, чтобы оценивать соответствие модели, я хотел бы просто привести модель в соответствие. Компромиссный подход состоит в том, чтобы предположить, что взаимодействия не важны, и позволить непрерывным предикторам быть нелинейными с помощью сплайнов регрессии. График предполагаемых отношений. rmsПакет в R делает все это относительно легко. Смотрите http://biostat.mc.vanderbilt.edu/rms для получения дополнительной информации.

Вы можете уточнить «пары» и то, являются ли ваши наблюдения независимыми.

Фрэнк Харрелл
источник

Если я правильно понимаю, ваш совет заключается в том, чтобы сосредоточиться на графике остатков и получить его прямо, прежде чем делать что-либо еще, в конечном итоге используя сплайны регрессии, я прав? Я отредактировал вопрос, чтобы указать, сколько существует предикторов и что пары «относительно» независимы.

Антуан Вернет

Привет, Фрэнк. Почему вы говорите, что точность классификации это плохой метод? Это потому, что здесь она оценивается по тем же данным, из которых получена модель?

Питер Флом - Восстановить Монику

χ^{2}

$\chi^2$

c

$c$

Нет, я имею в виду, что непрерывные предикторы могут работать нелинейно по шкале логарифмов, расширяя их в несколько терминов, используя ограниченные кубические сплайны (естественные сплайны). Затем составьте график предполагаемых преобразований, чтобы узнать о частичных эффектах каждого предиктора.

Фрэнк Харрелл

Спасибо за вклад, это было действительно полезно. Более подробно изучив данные, я понял, что у меня есть проблемы с коллинеарностью (даже если у меня не было высоких парных корреляций).

Антуан Верне

$x^2$

Gung - Восстановить Монику
источник