Класс сложности состоит из тех -проблем, которые могут быть решены недетерминированной машиной Тьюринга за полиномиальное время, которая имеет не более одного приемлемого вычислительного пути. То есть решение, если оно есть, является уникальным в этом смысле. Весьма маловероятно, что все -проблемы находятся в , потому что по теореме Валианта-Вазирани это будет означать коллапс .
С другой стороны, известно, что ни одна -проблема не является -полной, что говорит о том, что требование уникального решения все-таки делает их проще.
Я ищу примеры, где предположение об уникальности приводит к более быстрому алгоритму.
Например, глядя на проблемы с графом, можно ли найти максимальную клику в графе быстрее (хотя, возможно, все еще в экспоненциальном времени), если мы знаем, что граф имеет уникальную максимальную клику? Как насчет уникальной -цветности, уникального гамильтонова пути, уникального минимального доминирующего множества и т. Д.?
В общем, мы можем определить версию с уникальным решением для любой проблемы, связанной с , уменьшив ее до . Известно ли кому-либо из них, что добавление предположения об уникальности приводит к более быстрому алгоритму? (Допуская, что это все еще остается экспоненциальным.)



Ответы:
3-SAT может быть одной из таких проблем. В настоящее время лучшая верхняя граница для уникального 3-SAT экспоненциально быстрее, чем для обычного 3-SAT. (Ускорение является экспоненциальным, хотя уменьшение показателя незначительно.) Рекордсменом для уникального случая является эта статья Тимона Хертли.
Алгоритм Хертли основан на важном алгоритме PPSZ Патури , Пудлака, Сакса и Зейна для -SAT, который, я считаю, все еще является самым быстрым для (см. Также эту статью энциклопедии). Исходный анализ показал лучшие оценки для Unique -SAT, чем для общего -SAT, когда ; впоследствии, однако, Хертли показал в другой статье, что вы можете получить те же оценки для (слегка подправленного) алгоритма PPSZ, не предполагая уникальности. Так что, может быть, уникальность помогает, и это может определенно упростить анализ некоторых алгоритмов, но наше понимание роли уникальности для


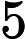








Существуют доказательства того, что Unique -SAT не намного проще, чем обычный -SAT. Гипотеза сильного экспоненциального времени (SETH) утверждает, что , так что переменная -SAT разрешима за времени для каждой константы . В статье Калабро, Импальяццо, Кабанца и Патури было показано , что если выполняется SETH, то то же самое утверждение верно для Unique -SAT. Кроме того, если для общего SAT требуется экспоненциальное время, то есть существует некоторое такое, что общееk δ < 1 n k O ∗ ( 2 δ n ) k ≥ 3 k k k ≥ 3 , ϵ > 0 k O ∗ ( 2 ϵ n )

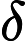








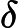











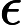







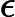


(Примечание: запись подавляет полиномиальные множители во входной длине.)

источник
Проблема кратчайших 2-вершинных непересекающихся путей в неориентированных графах, недавно решенная (ICALP14) А. Бьорклундом и Т. Хусфельдтом. Но детерминированное решение для случая существования единственного решения. В случае, когда существует более одного решения, они показали, что проблема принадлежит RP . Как упоминали авторы статьи, неизвестно, находится ли проблема в P в общем сценарии.
источник
Вне теории сложности и анализа алгоритмов предположение о том, что может быть только одно решение, формирует основу для некоторых стандартных правил, используемых для вывода решения в головоломках Судоку. Эти правила обычно включают в себя поиск путей, с помощью которых части головоломки могут иметь два или более решений, которые не взаимодействуют с остальной частью головоломки. Этого не может быть в реальном решении, поэтому, если шаблон, который угрожает вызвать это, найден, то он должен быть нарушен, что позволяет решающему устройству вывести ограничения на то, как может выглядеть фактическое решение. См. Http://www.brainbashers.com/sudokuuniquerectangles.asp, где приведены некоторые примеры правил вывода, основанных на уникальности.
источник
Упоминая еще один результат Бьёрклунда, если вам гарантировано, что в графе не более одного гамильтонова цикла, вы можете решить, является ли граф гамильтоновым быстрее, чем вы вообще можете.
Предположение об единственности означает, что соотношение числа Хэма. путь - это то же самое, что решить, является ли граф гамильтоновым.
Метод Бьёрклунда детерминистически вычисляет четность числа гамильтоновых циклов в то время как самый известный рандомизированный алгоритм для неориентированной гамильтоничности работает в , а лучший детерминированный алгоритм для направленной гамильтоничности (до насколько мне известно), это все еще 50-летний алгоритм динамического программирования Беллмана, Хелда и Карпа.O ∗ ( 1,665 n ) O ( n 2 2 n )




















источник