Из теоремы Ладнера хорошо известно, что если , то существует бесконечно много N P -интермедиантных ( N P I ) задач. Есть также естественные кандидаты на этот статус, такие как Изоморфизм графов и ряд других, см. Проблемы между P и NPC . Тем не менее, подавляющее большинство в толпе известной н в т у г а л Н Р -проблемы , как известно, быть либо в P или N P C . Лишь небольшая их часть остается кандидатом в Н П И , Другими словами, если мы случайно выберем естественную проблему среди известных, у нас будет очень мало шансов выбрать кандидата N P I. Есть ли объяснение этому явлению?
Я мог бы придумать 3 возможных объяснения, больше с философской стороны:
Причина, по которой такая малая доля естественных кандидатов состоит в том, что в конечном итоге N P I окажется пустой. Я знаю, это подразумевает P = N P , поэтому это очень маловероятно. Тем не менее, можно все еще утверждать (хотя я не один из них), что редкость естественных проблем N P I является эмпирическим наблюдением, которое, кажется, фактически поддерживает P = N P , в отличие от большинства других наблюдений.
Малость "натурального " представляет собой своего рода резкий фазовый переход между легкими и трудными проблемами. По-видимому, значимые, естественные алгоритмические проблемы ведут себя так, что они, как правило, либо легкие, либо сложные, переход узкий (но все же существует).
Аргумент в 2 могут быть приняты до крайности: в конечном счете , все проблемы в "естественно - " будет введен в Р ∪ N P C , пока P ≠ N Р , поэтому Н Р Я ≠ ∅ . Это будет означать, что все оставшиеся проблемы в N P Iявляются "неестественными" (придуманными, без реального смысла). Интерпретация этого может заключаться в том, что естественные проблемы либо легкие, либо сложные переход - только логическая конструкция, без «физического» значения. Это несколько напоминает случай иррациональных чисел, которые совершенно логичны, но не возникают как измеренное значение какой-либо физической величины. Как таковые, они не происходят из физической реальности, они скорее находятся в «логическом замыкании» этой реальности.
Какое объяснение тебе нравится больше или ты можешь предложить другое?
источник




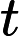
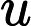





Ответы:
Как уже отмечалось, это спорно , в какой степени , что вы пытаетесь объяснить даже верно. Можно утверждать, что в 60-х и 70-х годах теоретиков-компьютерщиков просто больше интересовали проблемы, которые, как оказалось, связаны либо с P, либо с NP-полнотой. Сегодня, из-за роста теории сложности криптографии, квантовых вычислений, решеток и т. Д., А также простого факта, что NP-полнота стала настолько понятной - мы стали все больше и больше интересоваться виды проблем, которые оказываются NP-промежуточными.
Тем не менее, можно было бы спросить: до такой степени, что это правда, то есть до такой степени, что так много естественных проблем поиска и оптимизации «привязываются» к тому, чтобы быть либо NP-завершенными, либо еще в P - до такой степени , почему это так? Здесь, я думаю, вы можете получить большую интуицию, взглянув на более ранний феномен вычислимости: так много естественных моделей вычислений «привязываются» к полноте по Тьюрингу. В этом случае я бы сказал, что объяснение состоит в том, что, если у вас есть несколько основных компонентов - память для чтения / записи, циклы, условные выражения и т. Д. - трудно избежатьвозможность моделировать машину Тьюринга и, следовательно, быть полной по Тьюрингу. Во многом таким же образом, как только ваша проблема поиска или оптимизации имеет несколько основных компонентов - наиболее важно, способность создавать «гаджеты», которые имитируют логические элементы, такие как AND, OR и NOT, - трудно избежать возможности кодировать SAT и, следовательно, быть NP-полным.
Как мне нравится думать, такие проблемы, как SAT, оказывают сильное «гравитационное воздействие» на все другие вычислительные проблемы, которые их окружают, заставляя их хотеть «привязаться» к NP-завершению. Таким образом, обычно даже не требуется специального объяснения, когда еще одна проблема уступает этой тяге! Более поразительным и более нуждающимся в объяснении является то, что (очевидно) жесткая проблема NP имеет свойство, которое позволяет ей противостоять гравитационному притяжению SAT. Затем мы хотим знать , что это это свойство? Почему вы не можете разыграть обычную уловку NP-полноты для этой задачи - создать гаджеты, которые кодируют логические логические элементы? Я составил список некоторых общих ответов на этот вопрос в этом недавнем ответе CS.SE, но (как уже заметил другой комментатор) есть и другие возможные ответы, которые я пропустил.
источник
Многие естественные проблемы могут быть выражены как проблемы удовлетворения ограничений, и для CSP существуют теоремы о дихотомии.
источник
Просто шутка: после размышления о «гравитационном притяжении SAT» в приятном ответе Скотта Ааронсона мне в голову пришла другая метафора: сэндвич 3-SAT 2-SAT !
... но я не знаю, можно ли заполнить бутерброд натуральными ингредиентами (однако я обнаружил, что он может быть наполнен некоторыми -SAT соус [1], если гипотеза экспоненциального времени верна) :-D
Другой результат в [1] состоит в том, что он не может быть заполнен .







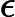




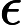


[1] Yunlei Zhao, Xiaotie Deng, CH Lee, Hong Zhu, -SAT и его свойства







источник
Рекомендации :
1- М. Грохе. Сложность проблем гомоморфизма и удовлетворения ограничений видна с другой стороны. Журнал ACM, 54 (1), статья 1, 2007
2- Питер Йонссон, Виктор Лагерквист и Густав Нордх. Выдувающие отверстия в различных аспектах вычислительных задач с приложениями к удовлетворению ограничений. В материалах 19-й Международной конференции по принципам и практике программирования ограничений (CP-2013). 2013.
источник
Вот сказка о структуре Златовласки НП-промежуточных задач. (Предупреждение: эта история может быть полезной ошибкой для генерации и проверки потенциальных гипотез, но она не предназначена для научной строгости. Она опирается на одну часть Гипотезы экспоненциального времени, черты колмогоровской магии сложности, некоторые фрагменты заимствованы из теории SAT решение и эвристическая трихотомия Теренса Тао для задач. Потребляйте на свой страх и риск, как и в случае со всеми ручными махинациями в математике.)
Если почти все экземпляры в задаче в NP хорошо структурированы, то проблема на самом деле в P. Таким образом, почти все экземпляры содержат много избыточности, и алгоритм задачи за полиномиальное время - это способ выделить избыточность. Можно даже предположить, что каждую проблему в P можно получить, взяв некоторую проблему в EXP и добавив некоторую структурированную избыточность через некоторую форму заполнения (не обязательно обычного вида). Если бы это было так, то алгоритм полиномиального времени мог бы рассматриваться как эффективный способ отменить это заполнение.
Если существует достаточно примеров, которые не структурированы, образуя «ядро твердости», то проблема является NP-полной.
Однако, если это «ядро твердости» слишком мало, то у него есть место только для представления некоторого SAT, поэтому проблема в P или NP-промежуточном звене. (Этот аргумент является сущностью теоремы Ладнера). Чтобы использовать аналогию Скотта, «ядро твердости» оказывает гравитационное воздействие на проблему, поскольку она является NP-полной. Экземпляры в «ядре жесткости» не содержат большой избыточности, и единственным реалистичным алгоритмом, который работает для всех этих экземпляров, является поиск методом «грубой силы» (конечно, если их только конечное число, поиск таблиц также работает).
С этой точки зрения, NP-промежуточные проблемы должны быть редкими на практике, поскольку они требуют хорошего баланса Златовласки между экземплярами, которые структурированы и неструктурированы. Экземпляры должны иметь достаточную избыточность, чтобы они были частично поддаются алгоритму, но должно быть достаточно ядра твердости, чтобы проблема не была в P.
Можно рассказать еще более простую (и забавную, но потенциально еще более вводящую в заблуждение) историю, основанную на головоломках. С помощью всего лишь нескольких ограничений можно выполнить большой поиск, например, NxN Sudoku является NP-полной. Теперь рассмотрите вопрос о том, чтобы вас попросили решить множество маленьких головоломок за один раз, например, за 9x9 Sudokus. Требуемое время будет примерно линейным по количеству головоломок в каждом случае, и эта проблема затем в P. Для промежуточных задач можно представить, что каждый случай является большим (но не слишком большим) числом судок на большом языке. (но не слишком большие) сетки. Причина, по которой мы не наблюдаем много таких проблем, заключается в том, что их было бы скучно представлять и решать!
источник
источник