Многие считают, что . Однако мы только знаем, что находится на втором уровне полиномиальной иерархии, то есть . Шаг к показу состоит в том, чтобы сначала перевести его на первый уровень полиномиальной иерархии, то есть .
Сдерживание будет означать, что недетерминизм по меньшей мере так же силен, как случайность в течение полиномиального времени.
Это также означает, что если для задачи мы можем найти ответы, используя эффективные (за полиномиальное время) рандомизированные алгоритмы, то мы можем эффективно проверить ответы (за полиномиальное время).
Есть ли какие-нибудь интересные интересные последствия для ?
Есть ли основания полагать, что доказательство сейчас недоступно (например, барьеры или другие аргументы)?


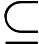




Ответы:
С одной стороны, доказательство будет легко означать, что , что уже означает, что ваше доказательство не может быть релятивизировано.


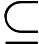










Но давайте посмотрим на что-то еще более слабое: . Если это так, то проверка полиномиальной идентичности для арифметических схем проводится в недетерминированное субэкспоненциальное время. Согласно Impagliazzo-Kabanets'04 , такой алгоритм подразумевает нижние границы схемы: либо у Permanent нет арифметических схем, либо .



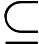


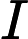





















Лично я не знаю, почему это выглядит «вне досягаемости», но это трудно доказать. Конечно, некоторые действительно новые уловки будут необходимы, чтобы доказать это.
источник