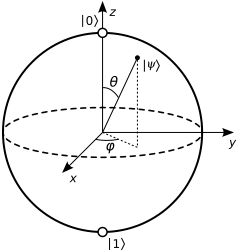
Как думать о Z воротах в блоховской сфере?

10

Я не совсем понимаю, как понимать врата в блоховской сфере. $Z$

Учитывая матрицу понятно, что и , $Z = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix}$ $Z|0\rangle = |0\rangle$ $Z|1\rangle = -|1\rangle$

Это объясняется здесь , что ворота вращение вокруг оси. Тогда как мне понимать ? Поскольку - южный полюс, я думаю, что естественно думать, что вращение вокруг оси ничего не делает. $Z$ $\pi$ $Z$ $Z|1\rangle = -|1\rangle$ $|1\rangle$ $\pi$ $Z$

quantum-gate bloch-sphere Бик
источник

7

Способ представления о блоховской сфере с точки зрения матрицы плотности состояния. действует наилиничего не делает, как это верно для любой диагональной матрицы плотности. Чтобы увидеть эффект вращения, вам нужно посмотреть, как любая недиагональная матрица плотности изменяется на , например, $Z$ $|0\rangle\langle 0|$ $|1\rangle\langle 1|$ $Z$ $|+\rangle\langle +|$

DaftWullie
источник

7

$|1\rangle$ и назначаются одной и той же точке на сфере Блоха, потому что они равны глобальной фазе . Алгебраически: где означает «равный глобальной фазе». Это значит, что есть такая такая, что . $-|1\rangle$ $|1\rangle \equiv -|1\rangle$ $\equiv$ $\theta$ $-|1\rangle = e^{i \theta} |1\rangle$

Вас смущает то, что, несмотря на то, что и , это не так для линейных комбинаций двух. Например, хотя . $|0\rangle \equiv Z |0\rangle$ $|1\rangle \equiv Z |1\rangle$ $Z |+\rangle \not\equiv Z |+\rangle$ $|+\rangle = \frac{1}{\sqrt{2}}|0\rangle + \frac{1}{\sqrt{2}}|1\rangle$

Крейг Гидни
источник

2

Согласно Википедии , мы можем написать любое чистое состояние как

| ψ ⟩ = \cos (\frac{θ}{2}) | 0 ⟩ + e^{i ϕ} \sin (\frac{θ}{2}) | 1 ⟩

$|\psi\rangle = \cos\left( \frac{\theta}{2} \right) |0 \rangle + e^{i \phi} \sin\left( \frac{\theta}{2} \right) |1 \rangle$

Где и - углы на сфере Блоха: $\theta$ $\phi$

Почти любая точка на поверхности (т.е. чистое состояние) имеет уникальное представление в терминах углов, за исключением полюсов. Как и на Земле, у Южного полюса нет четко определенной долготы (любая долгота работает одинаково), для состояния любая фаза означает то же самое. «Широта» здесь , давайте включим это в уравнение: $|1 \rangle$ $\phi$ $\theta$ $\pi$

| 1 ⟩ = \cos (\frac{π}{2}) | 0 ⟩ + e^{i ϕ} \sin (\frac{π}{2}) | 1 ⟩ =

$|1\rangle = \cos\left( \frac{\pi}{2} \right) |0 \rangle + e^{i \phi} \sin\left( \frac{\pi}{2} \right) |1 \rangle =$

= 0 + e^{i ϕ} | 1 ⟩

$= 0 + e^{i \phi} |1 \rangle$

Если вы знакомы с личностью Эйлера, вы, вероятно, узнаете как вращение в комплексной плоскости. В частности, поскольку является поворотом для , мы получаем знаменитое , в конечном итоге получая . $e^{i \phi}$ $Z$ $\phi = \pi$ $e^{i \pi} = -1$ $|1 \rangle = - |1 \rangle$

Norrius
источник

1

Это не верно. Запись вводит в заблуждение: это эквивалентные состояния в том смысле, что они отличаются только глобальной фазой, но это не означает, что векторы состояния одинаковы. Вы получаете этот результат, потому что вы предполагаете, что между векторами состояния и точками на сфере Блоха существует биекция, а это не так. Биекция находится между точками на блоховской сфере и состояниями, описанными как матрицы плотности

| 1 ⟩ = - | 1 ⟩

$|1\rangle=-|1\rangle$

GLS

@glS Спасибо, который следует из этого, показался подозрительным. Имеет ли смысл улучшить этот ответ с вашей точки зрения, или это безнадежно неправильно?

1 = - 1

$1=-1$

Норриус

это ваш звонок =). Я думаю, что правильный ответ - тот, который дал DaftWullie (я полагаю, что у спрашивающего было такое же заблуждение, как и в вашем ответе). Я не вижу, что еще можно сказать по этому вопросу

GLS

Как думать о Z воротах в блоховской сфере?

Ответы: