Я только что прочитал о cycortort через сообщение в блоге sortvis.org. Это, вероятно, самый неясный вопрос, о котором я когда-либо слышал, поскольку в нем используется математика, с которой я не знаком (обнаружение циклов в перестановках целочисленных множеств).
Какой самый неизвестный из тех, кого ты знаешь?
algorithms
sorting
Шова
источник
источник

Ответы:
Вы когда-нибудь слышали о сортировке терпения ? Ну, теперь у вас есть ...
источник
Медленная сортировка работает путем умножения и сдачи (в отличие от разделяй и властвуй). Это интересно, потому что это, конечно, наименее эффективный алгоритм сортировки, который может быть построен (асимптотически и с ограничением, что такой алгоритм, будучи медленным, все равно должен все время работать для достижения результата).
Это смещает его от bogosort, потому что в лучшем случае bogosort достаточно эффективен, а именно, когда массив уже отсортирован. Slowsort не «страдает» от такого поведения в лучшем случае. Даже в лучшем случае он все еще имеет время выполнения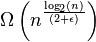 для ϵ > 0.
для ϵ > 0.
Вот его псевдокод, адаптированный из немецкой статьи в Википедии :
источник
Я не знаю, считается ли это неясным, но один из самых нелепых «алгоритмов» сортировки - Bogosort . Ссылки со страницы Bogosort тоже интересны.
И есть этот драгоценный камень из раздела «квантовый Bogo-сорт».
Хммм ... можно сказать и так :-).
источник
Еще один непонятный «алгоритм» - это Intelligent Design Sort - но ни один алгоритм не работает быстрее или потребляет меньше памяти :)
источник
Sleep Sort довольно нова.
источник
Я думаю, что пузырьковая сортировка была бы неправильным ответом и в этой ситуации.
:)
источник
Кнут Том 3 1 , в ответ на одно из упражнений, дает реализацию алгоритма безымянной сортировки, который по сути представляет собой древний гольф-код - самый короткий вид, который вы можете написать на ассемблере MIX. Короткий код действительно идет по очень незначительной цене сложности O (N 3 ), хотя ...
1 По крайней мере, в старых изданиях. Учитывая изменения в MIXAL для новой редакции, я не уверен, что он все еще там, или даже имеет небольшой смысл в оригинальной версии MIXAL.
источник
Для моего класса структур данных мне пришлось (явно) доказать правильность сортировки Штоге . Время работы O (n ^ {log 3 / log 1.5}) = O (n ^ 2.7095 ...).
источник
Я не знаю, является ли это самым неясным, но сорт спагетти - один из лучших в ситуациях, когда вы можете его использовать.
источник
Одна из оригинальных книг Кнута, «Сортировка и поиск», имела среднюю раскладку, которая представляла схему процесса, который сортировал файл на магнитной ленте без использования жесткого диска. Я думаю, что он использовал шесть ленточных накопителей и явно показывал, когда каждый читал вперед, читал назад, перематывал или работал вхолостую. Сегодня это памятник устаревшей технологии.
источник
Однажды я сделал пузырьковую сортировку в векторных регистрах в ассемблере CRAY. Машина имела команду двойного сдвига, которая позволяла вам сдвигать содержимое векторного регистра вверх / вниз на одно слово. Поместите все остальные точки в два векторных регистра, и тогда вы сможете выполнить полную пузырьковую сортировку, даже не делая другую ссылку на память, пока не закончите. За исключением N ** 2 природы пузырьковой сортировки, она была эффективной.
Мне также однажды потребовалось сделать сортировку вектора длины 4 с плавающей запятой как можно быстрее для одной сортировки. Сделано это путем поиска в таблице (знаковый бит A2-A1 равен одному биту, знак A3-A1 образует другой бит ..., затем вы просматриваете вектор перестановки в таблице. На самом деле это было самое быстрое решение, которое я мог найти с. Не работает на современных архитектурах, хотя, плавающие и целочисленные единицы слишком разделены.
источник
У Google Code Jam была проблема с алгоритмом под названием Gorosort, который, я думаю, они изобрели для этой проблемы.
http://code.google.com/codejam/contest/dashboard?c=975485#s=p3
источник
Не помню название, но это было в основном
источник
Сортировка оболочки
Может быть, сам алгоритм не так неясен, но кто может назвать реализацию, которая фактически используется на практике? Я могу!
TIGCC (компилятор на основе GCC для графических калькуляторов TI-89/92 / V200) использует сортировку Shell для
qsortреализации в своей стандартной библиотеке:Сортировка оболочки была выбрана в пользу быстрой сортировки, чтобы размер кода был низким. Хотя асимптотическая сложность еще хуже, TI-89 не имеет большого объема ОЗУ (190 Кбайт, за вычетом размера программы и общего размера любых неархивированных переменных), поэтому можно с уверенностью предположить, что количество элементов будет быть низким.
Более быстрая реализация была написана после того, как я пожаловался, что она слишком медленная в написанной мной программе. Он использует лучшие размеры зазоров, наряду с оптимизацией сборки. Его можно найти здесь: qsort.c
источник