Как бы я пошел о создании списка всех возможных перестановок строки между символами x и y длиной, содержащей список переменных символов.
Любой язык будет работать, но он должен быть переносимым.
string
language-agnostic
cross-platform
UnkwnTech
источник
источник

Ответы:
Есть несколько способов сделать это. Обычные методы используют рекурсию, запоминание или динамическое программирование. Основная идея заключается в том, что вы создаете список всех строк длины 1, а затем в каждой итерации для всех строк, созданных в последней итерации, добавляете эту строку, объединенную с каждым символом в строке по отдельности. (индекс переменной в приведенном ниже коде отслеживает начало последней и следующей итерации)
Какой-то псевдокод:
Затем вам нужно будет удалить все строки, длина которых меньше x, они будут первыми (x-1) * len (originalString) записями в списке.
источник
Лучше использовать возврат
источник
Вы получите много строк, это точно ...
Где x и y - это то, как вы их определяете, а r - количество символов, из которых мы выбираем - если я вас правильно понимаю. Вы должны определенно генерировать их по мере необходимости и не становиться неряшливыми, скажем, генерировать powerset и затем фильтровать длину строк.
Следующее, безусловно, не лучший способ для их создания, но, тем не менее, это интересный аспект.
Кнут (том 4, глава 2, 7.2.1.3) говорит нам, что (s, t) -комбинация эквивалентна s + 1 вещам, взятым t за один раз с повторением - (s, t) -комбинация - это обозначение, используемое Кнут, равный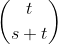 . Мы можем выяснить это, сначала сгенерировав каждую (s, t) -комбинацию в двоичной форме (т.е. длины (s + t)) и посчитав количество нулей слева от каждого 1.
. Мы можем выяснить это, сначала сгенерировав каждую (s, t) -комбинацию в двоичной форме (т.е. длины (s + t)) и посчитав количество нулей слева от каждого 1.
10001000011101 -> становится перестановкой: {0, 3, 4, 4, 4, 1}
источник
Нерекурсивное решение по примеру Кнута, Python:
источник
"54321"только ОДНА строкой предъявляются (сам).nextPermutation()имеет состояния - для перестановки требуется только ввод, и индексы не поддерживаются от итерации к итерации. Это можно сделать, предполагая, что начальный ввод был отсортирован, и найдя индексы (k0иl0) непосредственно в зависимости от того, где поддерживается порядок. Сортировка ввода типа «54321» -> «12345» позволит этому алгоритму найти все ожидаемые перестановки. Но так как он проделывает большую дополнительную работу по поиску этих индексов для каждой генерируемой перестановки, существуют более эффективные способы сделать это нерекурсивно.Вы можете посмотреть « Эффективное перечисление подмножеств набора », в котором описывается алгоритм, позволяющий выполнить часть того, что вы хотите - быстро сгенерировать все подмножества из N символов длиной от x до y. Он содержит реализацию на C.
Для каждого подмножества вам все равно придется генерировать все перестановки. Например, если вы хотите 3 символа из «abcde», этот алгоритм даст вам «abc», «abd», «abe» ... но вам нужно будет переставить каждый из них, чтобы получить «acb», «bac», "bca" и т. д.
источник
Некоторый рабочий Java-код, основанный на ответе Sarp :
источник
Вот простое решение в C #.
Он генерирует только различные перестановки данной строки.
источник
Здесь много хороших ответов. Я также предлагаю очень простое рекурсивное решение в C ++.
Примечание : строки с повторяющимися символами не будут производить уникальные перестановки.
источник
Я просто быстро все это написал в Ruby:
Вы могли бы взглянуть на API языка для встроенных функций типа перестановки, и вы могли бы написать более оптимизированный код, но если числа слишком велики, я не уверен, что есть много способов получить много результатов ,
В любом случае, идея кода заключается в том, чтобы начать со строки длины 0, а затем отслеживать все строки длины Z, где Z - текущий размер в итерации. Затем просмотрите каждую строку и добавьте каждый символ в каждую строку. Наконец, в конце удалите все, что было ниже порога x, и верните результат.
Я не проверял это с потенциально бессмысленным вводом (нулевой список символов, странные значения x и y и т. Д.).
источник
Это перевод версии Майка для Ruby на Common Lisp:
И другая версия, немного короче и использующая больше возможностей петли:
источник
Вот простое слово C # рекурсивное решение:
Метод:
Вызов:
источник
... а вот версия C:
источник
Печатает все перестановки без дубликатов
источник
Рекурсивное решение в C ++
источник
В Perl, если вы хотите ограничиться строчными буквами, вы можете сделать это:
Это дает все возможные строки от 1 до 4 символов, используя строчные буквы. Для заглавных букв измените
"a"на"A"и"zzzz"на"ZZZZ".Для смешанного случая это становится намного сложнее, и, вероятно, это невозможно сделать с помощью одного из встроенных операторов Perl, подобных этому.
источник
Рубиновый ответ, который работает:
источник
источник
Следующая рекурсия Java печатает все перестановки данной строки:
Ниже приводится обновленная версия вышеупомянутого метода "permut", который делает n! (n факториал) менее рекурсивные вызовы по сравнению с вышеуказанным методом
источник
Я не уверен, почему вы хотели бы сделать это в первую очередь. Результирующий набор для любых умеренно больших значений x и y будет огромным и будет экспоненциально расти по мере увеличения x и / или y.
Допустим, ваш набор возможных символов - это 26 строчных букв алфавита, и вы просите ваше приложение сгенерировать все перестановки, где длина = 5. Если вы не исчерпаете память, вы получите 11 881 376 (то есть, 26 на мощность). 5) струны назад. Увеличьте эту длину до 6, и вы получите 308 915 776 строк. Эти цифры становятся очень большими, очень быстро.
Вот решение, которое я собрал в Java. Вам нужно будет предоставить два аргумента времени выполнения (соответствующих x и y). Радоваться, веселиться.
источник
Вот нерекурсивная версия, которую я придумал, в javascript. Это не основано на нерекурсивном Кнуте выше, хотя у него есть некоторые сходства в обмене элементами. Я проверил его правильность для входных массивов до 8 элементов.
Быстрая оптимизация - это предварительная проверка
outмассива и избежаниеpush().Основная идея:
Для одного исходного массива создайте первый новый набор массивов, которые поочередно меняют первый элемент на каждый последующий элемент, каждый раз оставляя невозмущенные другие элементы. например: дано 1234, сгенерировано 1234, 2134, 3214, 4231.
Используйте каждый массив из предыдущего прохода в качестве начального числа для нового прохода, но вместо замены первого элемента меняйте местами второй элемент с каждым последующим элементом. Кроме того, на этот раз не включайте исходный массив в вывод.
Повторите шаг 2, пока не будет сделано.
Вот пример кода:
источник
В рубине:
Это довольно быстро, но это займет некоторое время =). Конечно, вы можете начать с "aaaaaaaa", если короткие строки вам не интересны.
Хотя, возможно, я неверно истолковал реальный вопрос - в одном из постов он звучал так, как будто вам просто нужна библиотека брутфорсов, но в основном вопрос звучит так, как будто вам нужно переставить определенную строку.
Ваша проблема в чем-то похожа на эту: http://beust.com/weblog/archives/000491.html (перечислите все целые числа, в которых ни одна из цифр не повторяется, что привело к тому, что ее решило множество языков, с ocaml парень, использующий перестановки, и некоторый парень java, использующий еще одно решение).
источник
Я нуждался в этом сегодня, и хотя ответы, которые уже были даны, указали мне правильное направление, они были не совсем тем, что я хотел.
Вот реализация, использующая метод Heap. Длина массива должна быть не менее 3, а по практическим соображениям - не более 10 или около того, в зависимости от того, что вы хотите сделать, терпения и тактовой частоты.
Перед тем, как ввести свой цикл инициализацию
Perm(1 To N)с первой перестановкой,Stack(3 To N)с нулями *, иLevelс2**. В конце вызова циклаNextPerm, который вернет false, когда мы закончим.* VB сделает это за вас.
** Вы можете немного изменить NextPerm, чтобы сделать это ненужным, но это более понятно.
Другие методы описаны различными авторами. Кнут описывает два, один дает лексический порядок, но сложен и медленен, другой известен как метод простых изменений. Цзе Гао и Дяньцзюнь Ван также написали интересную статью.
источник
Этот код в python, когда вызывается с
allowed_charactersустановленным значением[0,1]и максимум 4 символами, генерирует 2 ^ 4 результата:['0000', '0001', '0010', '0011', '0100', '0101', '0110', '0111', '1000', '1001', '1010', '1011', '1100', '1101', '1110', '1111']Надеюсь, что это полезно для вас. Работает с любым персонажем, а не только с цифрами
источник
Вот ссылка, которая описывает, как напечатать перестановки строки. http://nipun-linuxtips.blogspot.in/2012/11/print-all-permutations-of-characters-in.html
источник
Хотя это не дает точного ответа на ваш вопрос, вот один из способов генерировать каждую перестановку букв из ряда строк одинаковой длины: например, если ваши слова были «coffee», «joomla» и «moodle», вы можете ожидайте вывод, как "coodle", "joodee", "joffle" и т. д.
По сути, количество комбинаций - это (количество слов) в степени (количество букв на слово). Таким образом, выберите случайное число от 0 до количества комбинаций - 1, преобразуйте это число в основание (количество слов), а затем используйте каждую цифру этого числа в качестве индикатора, для которого нужно взять следующую букву.
например: в приведенном выше примере. 3 слова, 6 букв = 729 комбинаций. Выберите случайное число: 465. Преобразуйте в основание 3: 122020. Возьмите первую букву из слова 1, 2-ю из слова 2, 3-ю из слова 2, 4-у из слова 0 ... и вы получите ... "joofle".
Если вам нужны все перестановки, просто выполните цикл от 0 до 728. Конечно, если вы выбираете только одно случайное значение, гораздо
более простым именее запутанным способом будет циклическое перебирание букв. Этот метод позволяет вам избежать рекурсии, если вы хотите все перестановки, плюс он заставляет вас выглядеть так, как будто вы знаете математику (тм) !Если количество комбинаций чрезмерно, вы можете разбить его на серию более мелких слов и объединить их в конце.
источник
C # итеративный:
источник
источник
Вот мой взгляд на нерекурсивную версию
источник
Питоническое решение:
источник
Вот элегантное нерекурсивное решение O (n!):
источник