В настоящее время я готовлюсь к интервью, и это напомнило мне вопрос, который мне однажды задавали в предыдущем интервью, который звучал примерно так:
"Вас попросили разработать программное обеспечение для непрерывного отображения 10 самых популярных поисковых запросов в Google. Вам предоставляется доступ к фиду, который обеспечивает бесконечный поток поисковых запросов, которые в настоящее время ищут в Google, в реальном времени. Опишите, какой алгоритм и структуры данных вы бы использовали для этого. Вы должны разработать два варианта:
(i) Отображать 10 самых популярных поисковых запросов за все время (т. е. с тех пор, как вы начали читать ленту).
(ii) Отображать только 10 самых популярных поисковых запросов за последний месяц, обновляемых ежечасно.
Вы можете использовать аппроксимацию, чтобы получить список 10 лучших, но вы должны обосновать свой выбор ».
Я провалился в этом интервью и до сих пор понятия не имею, как это реализовать.
В первой части запрашиваются 10 наиболее часто встречающихся элементов в постоянно растущей подпоследовательности бесконечного списка. Я изучил алгоритмы выбора, но не нашел онлайн-версий для решения этой проблемы.
Во второй части используется конечный список, но из-за большого объема обрабатываемых данных вы не можете хранить в памяти весь месяц поисковых запросов и вычислять гистограмму каждый час.
Проблема усложняется тем фактом, что список топ-10 постоянно обновляется, поэтому вам нужно каким-то образом подсчитывать свои топ-10 в скользящем окне.
Любые идеи?

what is the most frequent item in the subsequence [2; 2; 3; 3; 3; 4; 4; 4; 4; 5; 5] of your sequence?Ответы:
Что ж, похоже, очень много данных с, возможно, непомерно высокой стоимостью хранения всех частот. Когда объем данных настолько велик, что мы не можем надеяться сохранить их все, мы переходим в область алгоритмов потоков данных .
Полезная книга в этой области: Мутукришнан - «Потоки данных: алгоритмы и приложения»
Тесно связанная ссылка на рассматриваемую проблему, которую я выбрал из приведенного выше: Манку, Мотвани - «Приблизительный подсчет частоты в потоках данных» [pdf]
Между прочим, Мотвани из Стэнфорда (править) был автором очень важной книги «Рандомизированные алгоритмы» .
Этой проблеме посвящена 11-я глава этой книги. Изменить: извините, плохая ссылка, эта конкретная глава посвящена другой проблеме. После проверки, вместо этого я рекомендую раздел 5.1.2 Muthukrishnan в книге , доступны в Интернете.Хех, хороший вопрос для интервью.
источник
Обзор оценки частоты
Есть несколько хорошо известных алгоритмов, которые могут предоставить оценки частоты для такого потока, используя фиксированный объем памяти. Один из них - часто, Мисра и Грис (1982). Из списка из n элементов он находит все элементы, которые встречаются более n / k раз, используя счетчики k - 1 . Это обобщение алгоритма большинства Бойера и Мура (Fischer-Salzberg, 1982), где k равно 2. Алгоритмы LossyCounting (2002) Манку и Мотвани и SpaceSaving (2005) Метвалли имеют схожие требования к пространству, но могут обеспечить более точные оценки при определенных условиях. условия.
Важно помнить, что эти алгоритмы могут предоставлять только оценки частоты. В частности, оценка Misra-Gries может занижать фактическую частоту на (n / k) пунктов.
Предположим, у вас есть алгоритм, который может положительно идентифицировать элемент только в том случае, если он встречается более чем в 50% случаев. Подайте в этот алгоритм поток из N различных элементов, а затем добавьте еще N - 1 копию одного элемента, x , всего 2N - 1 элементов. Если алгоритм сообщает вам, что x превышает 50% от общего количества, это должно быть в первом потоке; если нет, значит x не было в исходном потоке. Чтобы алгоритм сделал это определение, он должен сохранить исходный поток (или некоторую сводку, пропорциональную его длине)! Таким образом, мы можем доказать себе, что пространство, необходимое для такого «точного» алгоритма, будет Ω ( N ).
Вместо этого описанные здесь частотные алгоритмы предоставляют оценку, идентифицируя любой элемент, который превышает пороговое значение, а также некоторые элементы, которые опускаются ниже этого порога с определенным запасом. Например, алгоритм большинства , использующий один счетчик, всегда дает результат; если какой-либо элемент превышает 50% потока, он будет найден. Но он также может дать вам элемент, который встречается только один раз. Вы бы не узнали этого, не сделав второй проход по данным (опять же, используя один счетчик, но ища только этот элемент).
Частый алгоритм
Вот простое описание Мишра-Грис Частого алгоритм. Demaine (2002) и другие оптимизировали алгоритм, но это дает вам суть.
Укажите пороговую долю, 1 / k ; будет найден любой элемент, который встречается более n / k раз. Создайте пустую карту (например, красно-черное дерево); ключи будут условиями поиска, а значения будут счетчиком для этого термина.
Обратите внимание, что вы можете обрабатывать бесконечный объем данных с фиксированным объемом хранилища (только карта фиксированного размера). Требуемый объем памяти зависит только от интересующего порога, а размер потока не имеет значения.
Подсчет поисков
В этом контексте, возможно, вы буферизуете один час поиска и выполните этот процесс на данных этого часа. Если вы можете сделать второй проход по журналу поиска за этот час, вы сможете получить точное количество вхождений лучших «кандидатов», идентифицированных на первом проходе. Или, может быть, это нормально - сделать один проход и сообщить обо всех кандидатах, зная, что любой элемент, который должен быть там, включен, а любые дополнения - это просто шум, который исчезнет в следующий час.
Любые кандидаты, которые действительно превышают порог интереса, сохраняются в виде сводки. Сохраните эти сводки за месяц, отбрасывая самые старые каждый час, и вы получите хорошее приближение к наиболее распространенным запросам.
источник
Это один из исследовательских проектов, которые я сейчас прохожу. Требование почти такое же, как у вас, и мы разработали хорошие алгоритмы для решения этой проблемы.
Вход
Входные данные - это бесконечный поток английских слов или фраз (мы называем их
tokens).Выход
Применение этого исследования - найти горячую тему или тенденции в Twitter или Facebook. У нас есть сканер, который сканирует веб-сайт и генерирует поток слов, которые передаются в систему. Затем система выведет наиболее часто встречающиеся слова или фразы в целом или в прошлом. Представьте, что за последние пару недель фраза «Чемпионат мира» много раз появлялась в Твиттере. Так делает "осьминог Пол". :)
Строка в целые числа
В системе есть целочисленный идентификатор для каждого слова. Хотя в Интернете есть почти бесконечное количество возможных слов, но после накопления большого набора слов возможность поиска новых слов становится все меньше и меньше. Мы уже нашли 4 миллиона разных слов и каждому присвоили уникальный идентификатор. Весь этот набор данных может быть загружен в память в виде хэш-таблицы, занимающей примерно 300 МБ памяти. (Мы реализовали нашу собственную хеш-таблицу. Реализация Java требует огромных накладных расходов памяти)
Тогда каждую фразу можно идентифицировать как массив целых чисел.
Это важно, потому что сортировка и сравнение целых чисел намного быстрее, чем строк.
Архивные данные
В системе хранятся архивные данные по каждому токену. В основном это пары
(Token, Frequency). Однако таблица, в которой хранятся данные, будет настолько огромной, что нам придется физически разделить ее. Однажды схема разбиения основана на ngram токена. Если токен представляет собой одно слово, это 1 грамм. Если токен состоит из двух слов, это 2грамма. И это продолжается. Приблизительно в 4 граммах у нас есть 1 миллиард записей с размером таблицы около 60 ГБ.Обработка входящих потоков
Система будет поглощать поступающие предложения до тех пор, пока память не будет полностью использована (Да, нам нужен MemoryManager). После набора N предложений и сохранения в памяти система приостанавливает работу и начинает размечать каждое предложение в слова и фразы. Считается каждый жетон (слово или фраза).
Для очень часто используемых токенов они всегда хранятся в памяти. Для менее часто используемых токенов они сортируются по идентификаторам (помните, что мы переводим String в массив целых чисел) и сериализованы в файл на диске.
(Однако для вашей проблемы, поскольку вы считаете только слова, вы можете поместить всю карту частотности слов только в память. Тщательно разработанная структура данных будет занимать только 300 МБ памяти для 4 миллионов разных слов. Небольшой совет: используйте ASCII char для представляют строки), и это вполне приемлемо.
Между тем, будет другой процесс, который будет активирован, как только он найдет любой файл на диске, созданный системой, а затем начнет его объединение. Поскольку файл на диске отсортирован, для слияния потребуется такой же процесс, как и для сортировки слияния. Здесь также нужно позаботиться о некотором дизайне, поскольку мы хотим избежать слишком большого количества случайных поисков диска. Идея состоит в том, чтобы избежать одновременного чтения (процесс слияния) / записи (системный вывод) и позволить процессу слияния читать с одного диска при записи на другой диск. Это похоже на реализацию блокировки.
Конец дня
В конце дня в системе будет много часто используемых токенов с частотой, хранящихся в памяти, и множество других менее часто используемых токенов, хранящихся в нескольких дисковых файлах (и каждый файл будет отсортирован).
Система сбрасывает карту в памяти в файл на диске (отсортирует его). Теперь проблема становится объединением набора отсортированных файловых дисков. Используя аналогичный процесс, в конце мы получим один отсортированный дисковый файл.
Затем последняя задача - объединить отсортированный дисковый файл с архивной базой данных. В зависимости от размера архивной базы данных алгоритм работает, как показано ниже, если он достаточно большой:
Интуиция подсказывает, что через какое-то время количество вставок будет становиться все меньше и меньше. Все больше и больше операций будет идти только на обновление. И это обновление не будет наказываться index.
Надеюсь, все это объяснение поможет. :)
источник
Вы можете использовать хеш-таблицу в сочетании с двоичным деревом поиска . Реализовать
<search term, count>словарь, который сообщает вам, сколько раз каждый поисковый запрос был найден.Очевидно, что перебирать всю хеш-таблицу каждый час, чтобы получить 10 лучших, очень плохо. Но мы говорим об Google, поэтому вы можете предположить, что все десять лучших получат, скажем, более 10 000 обращений (хотя это, вероятно, намного большее число). Поэтому каждый раз, когда количество поискового запроса превышает 10 000, вставляйте его в BST. Затем каждый час вам нужно получать только первые 10 из BST, которые должны содержать относительно мало записей.
Это решает проблему попадания в топ-10 за все время.
Действительно сложная часть связана с тем, что один термин занимает место другого в ежемесячном отчете (например, «переполнение стека» может иметь 50 000 обращений за последние два месяца, но только 10 000 за последний месяц, а «amazon» может иметь 40 000 за последние два месяца, но 30 000 за последний месяц. Вы хотите, чтобы слово «amazon» было перед «переполнением стека» в ежемесячном отчете). Для этого я бы сохранил для всех основных (более 10 000 запросов за все время) поисковых запросов 30-дневный список, в котором будет указано, сколько раз этот запрос искали каждый день. Список будет работать как очередь FIFO: вы удаляете первый день и вставляете новый каждый день (или каждый час, но тогда вам может потребоваться хранить больше информации, что означает больше памяти / места. Если память не является проблемой, сделайте это, иначе пойти на это "приближение"
Похоже, это хорошее начало. Затем вы можете беспокоиться об удалении терминов, которые имеют> 10 000 совпадений, но их не было много в течение длительного времени, и тому подобное.
источник
случай i)
Поддерживайте хеш-таблицу для всех поисковых запросов, а также отсортированный список первой десятки отдельно от хеш-таблицы. Каждый раз, когда происходит поиск, увеличивайте соответствующий элемент в хеш-таблице и проверяйте, должен ли этот элемент теперь переключаться на 10-й элемент в списке первой десятки.
O (1) поиск для списка первой десятки и max O (log (n)) вставка в хеш-таблицу (при условии, что коллизии управляются самобалансирующимся двоичным деревом).
случай ii) Вместо того, чтобы поддерживать огромную хеш-таблицу и небольшой список, мы поддерживаем хеш-таблицу и отсортированный список всех элементов. Каждый раз, когда выполняется поиск, этот термин увеличивается в хэш-таблице, и в отсортированном списке термин может быть проверен, чтобы увидеть, должен ли он переключаться с термином после него. Для этого может хорошо работать самобалансирующееся двоичное дерево, так как нам также необходимо иметь возможность быстро запрашивать его (подробнее об этом позже).
Кроме того, мы также ведем список «часов» в виде списка FIFO (очереди). Каждый элемент «час» будет содержать список всех поисков, выполненных за этот конкретный час. Так, например, наш список часов может выглядеть так:
Затем каждый час: если список содержит не менее 720 часов (это количество часов в 30 дней), посмотрите на первый элемент в списке и для каждого поискового запроса уменьшите этот элемент в хеш-таблице на соответствующую величину. , После этого удалите этот элемент первого часа из списка.
Итак, допустим, у нас 721 час, и мы готовы взглянуть на первый час в нашем списке (выше). Мы бы уменьшили количество бесплатных материалов на 56 в хэш-таблице, смешные картинки на 321 и т. Д., А затем полностью удалили бы час 0 из списка, так как нам больше не нужно будет смотреть на него снова.
Причина, по которой мы поддерживаем отсортированный список всех терминов, позволяющих выполнять быстрые запросы, заключается в том, что каждый час после того, как мы просматриваем поисковые запросы, полученные 720 часов назад, нам необходимо обеспечивать отсортировку списка первой десятки. Так, например, когда мы уменьшаем «свободный материал» в хеш-таблице на 56, мы проверяем его место в списке. Поскольку это самобалансирующееся двоичное дерево, все это может быть выполнено за время O (log (n)).
Изменить: жертвовать точностью ради места ...
Было бы полезно также реализовать большой список в первом, как и во втором. Тогда мы могли бы применить следующую оптимизацию пространства в обоих случаях: Запустить задание cron, чтобы удалить все, кроме верхних x элементов в списке. Это снизит потребность в пространстве (и, как следствие, ускорит запросы по списку). Конечно, это дало бы приблизительный результат, но это можно. x можно вычислить перед развертыванием приложения на основе доступной памяти и динамически скорректировать, если становится доступным больше памяти.
источник
Грубое мышление ...
В топ-10 за все время
Для 10 лучших за месяц, обновляемых ежечасно:
Эээ ... имеет смысл? Я не думал об этом, как в реальной жизни
Ах да, забыл упомянуть, ежечасное «копирование / выравнивание», необходимое для ежемесячной статистики, может фактически повторно использовать тот же код, что и для 10 лучших за все время, - приятный побочный эффект.
источник
Точное решение
Во-первых, решение, которое гарантирует правильные результаты, но требует много памяти (большая карта).
Вариант "на все времена"
Поддерживайте хэш-карту с запросами в качестве ключей и их счетчиками в качестве значений. Кроме того, ведите список из 10 наиболее частых запросов на данный момент и подсчитайте 10-е место по частоте (порог).
Постоянно обновляйте карту по мере чтения потока запросов. Каждый раз, когда счетчик превышает текущий порог, сделайте следующее: удалите 10-й запрос из списка «Топ-10», замените его запросом, который вы только что обновили, а также обновите порог.
Вариант «Прошлый месяц»
Сохраните тот же список «10 лучших» и обновите его так же, как указано выше. Также сохраните аналогичную карту, но на этот раз сохраните векторы 30 * 24 = 720 отсчетов (по одному на каждый час) в качестве значений. Каждый час выполняйте для каждого ключа следующее: удалите самый старый счетчик из вектора, добавьте новый (инициализированный 0) в конце. Удалите ключ с карты, если вектор полностью равен нулю. Также каждый час нужно с нуля рассчитывать список «Топ-10».
Примечание. Да, на этот раз мы сохраняем 720 целых чисел вместо одного, но ключей гораздо меньше (постоянный вариант имеет очень длинный хвост).
приближения
Эти приближения не гарантируют правильного решения, но потребляют меньше памяти.
источник
10 самых популярных поисковых запросов за последний месяц
Использование эффективного индексации памяти / структуры данных, такой как плотно упакованные попытки (из статей в Википедии о попытках ), приблизительно определяет некоторую связь между требованиями к памяти и n - числом терминов.
Если необходимая память доступна ( предположение 1 ), вы можете вести точную ежемесячную статистику и агрегировать ее каждый месяц во все временные статистические данные.
Здесь также есть предположение, что «последний месяц» интерпретируется как фиксированное окно. Но даже если месячное окно скользит, описанная выше процедура демонстрирует принцип (скольжение можно аппроксимировать фиксированными окнами заданного размера).
Это напоминает мне циклическую базу данных, за исключением того, что некоторые статистические данные рассчитываются «за все время» (в том смысле, что не все данные сохраняются; rrd объединяет периоды времени без учета деталей путем усреднения, суммирования или выбора максимальных / минимальных значений, в данной задаче теряется информация о низкочастотных элементах, которые могут привести к ошибкам).
Предположение 1
Если мы не можем поддерживать идеальную статистику за весь месяц, тогда мы должны быть в состоянии найти определенный период P, для которого мы сможем поддерживать идеальную статистику. Например, предположим, что у нас есть идеальная статистика за некоторый период времени P, который уходит в месяц n раз.
Идеальная статистика определяет функцию
f(search_term) -> search_term_occurance.Если мы сможем хранить
nв памяти все идеальные таблицы статистики, скользящую ежемесячную статистику можно будет рассчитать следующим образом:nидеальные таблицы статистики)Однако, если мы сохраним только 10 лучших на агрегированном уровне (ежемесячно), то мы сможем отбросить много данных из полной статистики за фиксированный период. Это уже дает рабочую процедуру, которая имеет фиксированные (при условии, что верхняя граница таблицы точных статистических данных для периода P) требования к памяти.
Проблема с описанной выше процедурой заключается в том, что если мы сохраняем информацию только о 10 лучших терминах для скользящего окна (аналогично для всех времен), тогда статистика будет правильной для поисковых запросов, пик которых наступает в период, но может не увидеть статистика по поисковым запросам, которые постоянно появляются с течением времени.
Это можно компенсировать, храня информацию о более чем 10 основных терминах, например, о 100 лучших терминах, надеясь, что первые 10 будут правильными.
Я думаю, что дальнейший анализ может связать минимальное количество вхождений, необходимое для того, чтобы запись стала частью статистики (что связано с максимальной ошибкой).
(При принятии решения, какие записи должны стать частью статистики, можно также отслеживать и отслеживать тенденции; например, если линейная экстраполяция вхождений в каждый период P для каждого срока говорит вам, что этот термин станет значимым через месяц или два, вы может уже начать его отслеживание. Аналогичный принцип применяется для удаления поискового запроса из отслеживаемого пула.)
Наихудший случай для вышеизложенного - это когда у вас много почти одинаково часто встречающихся терминов, и они все время меняются (например, если отслеживается только 100 терминов, то, если первые 150 терминов встречаются одинаково часто, но лучшие 50 чаще встречаются в первый месяц и чтобы через некоторое время статистика не велась правильно).
Также может быть другой подход, который не фиксируется в размере памяти (строго говоря, ни то, ни другое не указано выше), который будет определять минимальную значимость с точки зрения вхождений / периода (день, месяц, год, за все время), для которого нужно сохранить статистика. Это может гарантировать максимальную ошибку в каждой статистике во время агрегирования (снова см. Циклический алгоритм).
источник
А как насчет адаптации «алгоритма замены страницы часов» (также известного как «второй шанс»)? Я могу представить, что это будет работать очень хорошо, если поисковые запросы распределяются равномерно (это означает, что большинство поисковых запросов появляются регулярно, а не 5 миллионов раз подряд и никогда больше).
Вот визуальное представление алгоритма: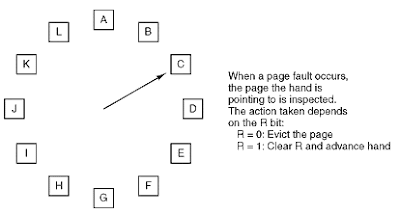
источник
Сохраните количество поисковых запросов в гигантской хеш-таблице, где каждый новый поиск приводит к увеличению определенного элемента на единицу. Следите за 20 или около того поисковыми запросами; когда элемент на 11-м месте увеличивается, проверьте, нужно ли ему поменять местами позиции с # 10 * (нет необходимости держать 10 лучших отсортированных; все, что вас волнует, - это провести различие между 10-м и 11-м).
* Аналогичные проверки должны быть выполнены, чтобы увидеть, находится ли новый поисковый запрос на 11-м месте, поэтому этот алгоритм переходит и к другим условиям поиска, поэтому я немного упрощаю.
источник
иногда лучший ответ - «не знаю».
Я сделаю более глубокий удар. Моим первым побуждением было бы передать результаты в Q. Процесс будет постоянно обрабатывать элементы, поступающие в Q. Процесс будет поддерживать карту
срок -> количество
каждый раз, когда обрабатывается Q-элемент, вы просто просматриваете поисковый запрос и увеличиваете счетчик.
В то же время я буду вести список ссылок на 10 самых популярных записей на карте.
Для записи, которая в настоящее время реализована, посмотрите, не превышает ли ее счетчик счетчика наименьшей записи в первой десятке (если ее еще нет в списке). Если это так, замените наименьшее записью.
Я думаю, это сработает. Никакая операция не требует много времени. Вам нужно будет найти способ управлять размером карты подсчета. но этого должно быть достаточно для ответа на интервью.
Они не ждут решения, они хотят посмотреть, сможете ли вы подумать. Вам не нужно сразу писать решение ...
источник
queue,Qэто буква :).Один из способов состоит в том, что для каждого поиска вы сохраняете этот поисковый запрос и его временную метку. Таким образом, поиск первой десятки за любой период времени - это просто вопрос сравнения всех поисковых запросов за данный период времени.
Алгоритм прост, но недостатком будет больший расход памяти и времени.
источник
Как насчет использования Splay Tree с 10 узлами? Каждый раз, когда вы пытаетесь получить доступ к значению (поисковому запросу), которого нет в дереве, выбрасывайте любой лист, вставляйте вместо него значение и обращайтесь к нему.
Идея этого та же, что и в моем другом ответе . При условии, что поисковые запросы используются равномерно / регулярно, это решение должно работать очень хорошо.
редактировать
Можно также сохранить в дереве еще несколько условий поиска (то же самое касается решения, которое я предлагаю в своем другом ответе), чтобы не удалять узел, который может быть снова доступен очень скоро. Чем больше значений хранится в нем, тем лучше результаты.
источник
Не знаю, правильно я это понимаю или нет. Мое решение использует кучу. Из-за 10 самых популярных элементов поиска я создаю кучу размером 10. Затем обновляю эту кучу с помощью нового поиска. Если частота нового поиска превышает верхнюю часть кучи (Max Heap), обновите ее. Откажитесь от того, с наименьшей частотой.
Но, как рассчитать частоту конкретного поиска, будем рассчитывать на другое. Может быть, как все заявили, алгоритм потока данных ....
источник
Используйте cm-sketch для хранения количества всех поисков с самого начала, оставьте min-heap размером 10 с ним для топ-10. Для ежемесячного результата сохраняйте 30 cm-sketch / hash-table и min-heap с ним, каждое начало подсчет и обновление за последние 30, 29 .., 1 день. По прошествии дня очистите последнее и используйте его как день 1. То же самое для почасового результата, сохраните 60 хеш-таблицы и минимальную кучу и начните отсчет последних 60, 59, ... 1 минуты. По прошествии минуты очистите последнее и используйте его как минуту 1.
Ежемесячный результат точен в пределах 1 дня, ежечасный результат точен в диапазоне 1 мин.
источник
Проблема не решается универсально, когда у вас есть фиксированный объем памяти и «бесконечный» (думаю, очень-очень большой) поток токенов.
Примерное объяснение ...
Чтобы понять, почему, рассмотрим поток токенов, который имеет конкретный токен (т. Е. Слово) T каждые N токенов во входном потоке.
Также предположим, что память может хранить ссылки (идентификатор слова и количество) не более чем на M токенов.
При этих условиях можно создать входной поток, в котором токен T никогда не будет обнаружен, если N достаточно велико, чтобы поток содержал разные M токенов между T.
Это не зависит от деталей алгоритма top-N. Это зависит только от лимита M.
Чтобы понять, почему это так, рассмотрим входящий поток, состоящий из групп двух идентичных токенов:
где a и b - все действительные токены, не равные T.
Обратите внимание, что в этом потоке T появляется дважды для каждого ai и bi. Тем не менее, его достаточно редко удалить из системы.
Начиная с пустой памяти, первый токен (T) займет слот в памяти (ограниченный M). Затем a1 будет занимать слот, вплоть до a- (M-1), когда M будет исчерпан.
Когда приходит aM, алгоритм должен отбросить один символ, пусть это будет T. Следующим символом будет b-1, что приведет к сбросу a-1 и т. Д.
Таким образом, T не будет оставаться резидентным в памяти достаточно долго, чтобы создать реальный счет. Короче говоря, любой алгоритм пропустит токен с достаточно низкой локальной частотой, но с высокой глобальной частотой (по длине потока).
источник