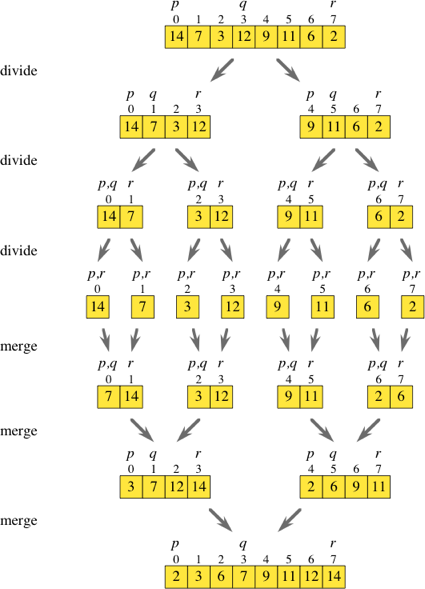
Таким образом, сортировка слиянием - это алгоритм «разделяй и властвуй». Пока я смотрел на приведенную выше диаграмму, я думал, можно ли вообще обойти все этапы разделения.
Если вы перебираете исходный массив при переходе на два, вы можете получить элементы по индексам i и i + 1 и поместить их в свои отсортированные массивы. Если у вас есть все эти подмассивы ([7,14], [3,12], [9,11] и [2,6], как показано на схеме), вы можете просто перейти к обычной процедуре слияния, чтобы получить отсортированный массив.
Является ли итерация по массиву и немедленная генерация требуемых подмассивов менее эффективной, чем выполнение шагов деления во всей их полноте?
algorithms
sorting
efficiency
mergesort
Jimmy_Rustle
источник
источник

Ответы:
Путаница возникает из-за разницы между концептуальным описанием алгоритма и его реализацией .
Логически сортировка слиянием описывается как разделение массива на более мелкие массивы, а затем их объединение. Однако «разбиение массива» не подразумевает «создание совершенно нового массива в памяти», или что-то в этом роде - это можно реализовать в коде как
т.е. никакой реальной работы не происходит, и «расщепление» является чисто концептуальным. Так что то, что вы предлагаете, безусловно, работает, но логически вы все еще «разбиваете» массивы - вам просто не нужна никакая работа с компьютера для этого :-)
источник
1<<n+1. Хотя я уверен, что вы можете отрегулировать вещи так, чтобы слишком маленький хвост слился с нижним проходом.Я предполагаю, что вы имеете в виду реализацию снизу вверх . В восходящей реализации вы начинаете с отдельных элементов ячейки и перемещаетесь вверх, объединяя элементы в большие отсортированные списки / массивы. Просто переверните стрелки на рисунке выше, начиная со среднего массива, то есть одноэлементных массивов.
Кроме того, вы можете оптимизировать сортировку слиянием , разделяя массивы, пока они не достигнут некоторого постоянного размера, после чего вы просто сортируете их, например, с помощью сортировки вставкой.
В противном случае сортировка без разбиения массива невозможна. Фактически сущность сортировки слиянием - это деление и сортировка подмассивов, т. Е. Разделяй и властвуй.
источник