Учитывая положительное число $n$ , найти количество алканов с $n$ атомами углерода, игнорируя стереоизомеры ; или, что эквивалентно, количество немеченых деревьев с $n$ узлами, так что каждый узел имеет степень $\le 4$ .

Это последовательность OEIS A000602 .

Смотри также: Парафины - Розетта Код

пример

Для $n = 7$ ответ $9$ , потому что гептан имеет девять изомеров :

• Гептан : $\mathrm{H_3C-CH_2-CH_2-CH_2-CH_2-CH_2-CH_3}$

• 2-метилгексан : $\mathrm{H_3C-CH(CH_3)-CH_2-CH_2-CH_2-CH_3}$

• 3-метилгексан : $\mathrm{H_3C-CH_2-CH(CH_3)-CH_2-CH_2-CH_3}$

• 2,2-диметилпентан : $\mathrm{H_3C-C(CH_3)_2-CH_2-CH_2-CH_3}$

• 2,3-диметилпентан : $\mathrm{H_3C-CH(CH_3)-CH(CH_3)-CH_2-CH_3}$

• 2,4-диметилпентан : $\mathrm{H_3C-CH(CH_3)-CH_2-CH(CH_3)-CH_3}$

• $\mathrm{H_3C-CH_2-C(CH_3)_2-CH_2-CH_3}$

• $\mathrm{H_3C-CH_2-C(CH_2CH_3)-CH_2-CH_3}$

• $\mathrm{H_3C-C(CH_3)_2-CH(CH_3)-CH_3}$

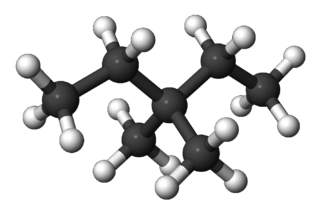
Обратите внимание, что 3-метилгексан и 2,3-диметилпентан являются хиральными , но здесь мы игнорируем стереоизомеры.

Контрольные примеры

$n = 0$

intput	output
=============
0	1
1	1
2	1
3	1
4	2
5	3
6	5
7	9
8	18
9	35
10	75
11	159
12	355
13	802
14	1858
15	4347
16	10359
17	24894
18	60523
19	148284
20	366319

CJam ( 100 98 91 89 83 байта)

1a{_[XX]*\_{_0a*}:E~\{E\_{ff*W%{0@+.+}*}:C~.+2f/}:D~.+C.+3f/1\+}q~:I*DE1$D.-X\+.+I=

Принимает ввод из стандартного ввода, выводит в стандартный вывод. Обратите внимание, что это использует лицензию, чтобы не обрабатывать ввод, 0чтобы сохранить два байта, вставляя определения Cи D. Онлайн демо

NB это очень медленно и неэффективно для памяти. Обрезка массивов позволяет получить более быструю версию (на 3 байта больше). Демо онлайн .

рассечение

$$\begin{eqnarray} A000598(x) &=& 1 + x Z(S_3; A000598(x)) \\ A000678(x) &=& x Z(S_4; A000598(x)) \\ A000599(x) &=& Z(S_2; A000598(x) - 1) \\ A000602(x) &=& A000678(x) - A000599(x) + A000598(x^2) \\ \end{eqnarray}$$ $Z(S_n; f(x))$$S_n$$f(x)$

Я манипулировал этим в немного разложенном по гольфу разложении, а затем посмотрел промежуточные последовательности и обнаружил, что они также находятся в OEIS:

$$\begin{eqnarray} A000642(x) &=& Z(S_2, A000598(x)) \\ A000631(x) &=& Z(S_2, A000642(x)) \\ A000602(x) &=& A000642(x) + x A000642(x^2) - x A000631(x) \end{eqnarray}$$

Более ранние версии повторно использовали блок C(сворачивать два полинома) из этого ответа . Я нашел намного более короткий, но я не могу обновить этот ответ, потому что это из цепочки вопросов.

1a            e# Starting from [1]...
{             e# Loop I times (see below) to build A000598 by f -> 1 + Z(S_3; f)
  _[XX]*      e#   Copy and double-inflate to f(x^3)
  \_          e#   Flip and copy: stack is f(x^3) f(x) f(x)
  {_0a*}:E~   e#   Assign copy-and-inflate to E and execute
              e#   Stack: f(x^3) f(x) f(x) f(x^2)
  \           e#   Flip
  {           e#   Define and execute block D, which applies f -> Z(S_2;f)
              e#     Stack: ... f
    E\_       e#     Stack: ... f(x^2) f(x) f(x)
    {         e#     Define and execute block C, which convolves two sequences
      ff*     e#       Multiply copies of the second sequence by each term of the first
      W%      e#       Reverse
      {       e#       Fold
        0@+.+ e#         Prepend a 0 to the first and pointwise sum
      }*
    }:C~      e#     Stack: ... f(x^2) f(x)^2
    .+2f/     e#     Pointwise average
  }:D~        e#   Stack: f(x^3) f(x) f(x^2) Z(S_2;f(x))
  .+C         e#   Stack: f(x^3) f(x)*(f(x^2) + Z(S_2;f(x)))
  .+3f/       e#   Add and divide by 3 to finish computing Z(S_3; f)
  1\+         e#   Prepend a 1
}
q~:I          e# Read input to I
*             e# Loop that many times
              e# Stack: I+1 terms of A000598 followed by junk
D             e# Stack: I+1 terms of A000642 followed by junk
E1$D          e# Stack: A000642 A000642(x^2) A000631
.-X\+.+       e# Stack: A000602
I=            e# Extract term I

Node.js 11,6,0 ,  229 223 221  218 байт

Получено из реализации Java, предложенной в Rosetta Code .

f=(N,L=1,u=[...r=[c=[],1,...Buffer(N)]],k=u[(g=(n,B,S,i,b=B,m,d=0)=>{for(;++b<5;)for(x=c[B]=(d+r[m=n])*(d++?c[B]/d:i),u[S+=n]+=L*2<S&&x,r[S]+=b<4&&x;--m;)g(m,b,S,c[B])})(L,0,1,1),L]-=~(x=r[L++/2])*x>>1)=>L>N?k:f(N,L,u)

Попробуйте онлайн!

Алхимик (1547 байт)

_->In_NN+2b+al+g
al+g+0NN->ak
al+g+NN->ah
ah+b->ah+m+d+z+a
ah+0b->C+Z+Q
Z+j+z->Z+j+d
Z+j+0z->M+s
M+g+b->M+g+r
M+g+h->M+g+d
M+g+0b+0h+q->J+U
J+o+h->J+o+m
J+o+a->J+o+d
J+o+0h+0a->2C+an+Q
an+j+h->an+j+d
an+j+0h->aC+s
aC+g->e+am+P
am+l+b->am+l+d
am+l+0b->al+s
ak+b->ak+m+d
ak+0b->C+aj+Q
aj+j+h->aj+j+b
aj+j+0h->I+n
I+f+e->I+f+a
I+f+b->I+f+m+d+z
I+f+0e+0b->C+ai+Q
ai+j+h->ai+j+b
ai+j+0h->aB+n
aB+f->H
H+z->H+d
H+a+e->H
H+0z+0e->G+i
G+i+0b->ag
G+i+b->az+b+n
az+f+0b->Out_a
az+f+b->G+b+n
G+f->G+t
ag+e->ag
ag+0e->af+t
af+i+e->af+i+a
af+i+0e->Out_a
Q->F+s
F+g+b->F+g+y
F+g+A->F+g
F+g+0b+0A->av+o
av+o+0m->w
av+o+m->m+ae+A
ae+m->ae+b
ae+0m->u+n
u+f+b->u+f+m
u+f+e->u+f+E
u+f+A->u+f+k+c
u+f+0b+0e+0A->ad
ad+c->ad+A
ad+0c->ac
ac+y->ac+d+c
ac+0y->ab
ab+c->ab+y
ab+0c->V+l
V+l+0k->x
V+l+k->aa+t
aa+i+0e->W
aa+i+e->Y
Y+E->Y+D+c
Y+0E->X
X+c->X+E
X+0c->aa+i
W+D->W+e
W+0D->V+P
x+E->x
x+d->x
x+b->x+k
x+0E+0d+0b->aw
aw+h->aw+d
aw+0h->aE+s
aE+g->p
p+b->p+2r
p+k->p+d
p+B->p
p+q->p
p+0b+0k+0B+0q->r+q+av+U
w+h->w+d
w+y->w+r
w+C->w+B+q
w+0h+0y+0C->aD+U
aD+o->j
U->au+s
au+g+b->au+g+d
au+g+0b->v
v+d->d+aA+t
aA+i+k->R
aA+i+0k->at
at+B->at+k+c
at+0B->L
L+c->L+B
L+r->L+b
L+0c+0r->as+n
as+f+b->as+f+r
as+f+0b->R
R+0e->K
R+e+q->ar+D+c
ar+e+q->ar+c
ar+0q->aq
aq+c->aq+q
aq+0c->R
K+D->K+e
K+h->K+b
K+0D+0h->ap+P
ap+l+b->ap+l+h
ap+l+0b->v
v+0d+k->v
v+0d+r->v
v+0d+0k+0r->o
s+0d->g
s+d->d+ao+t
ao+i->ao+P
ao+l->s
P->O+c
O+b->2c+O
O+0b->N
N+c->b+N
N+0c+e->O
N+0c+0e->l
n+b->n+c
n+0b->T
T+c->ay
T+0c->e+n
ay+c->b+T
ay+0c->f
t+d->t+c
t+0d->S
S+c->ax
S+0c->e+t
ax+c->d+S
ax+0c->i

Демо онлайн .

Примечание: это довольно медленно. Если вы тестируете с помощью интерпретатора, который поддерживает применение правила несколько раз одновременно (например, мой - хотя убедитесь, что у вас установлена ​​последняя версия, исправляющая ошибку в синтаксическом анализаторе), вы можете значительно ускорить процесс, добавив два правила:

T+2c->b+T
S+2c->d+S

которые встраивают маршрут через существующие правила

T+c->ay
ay+c->b+T
S+c->ax
ax+c->d+S

Частичное вскрытие

На высоком уровне это использует тот же подход, что и мой ответ CJam.

Вычислительная модель Алхимика по сути является машиной регистра Минского . Тем не менее, Alchemist очень хорошо раскрывает эквивалентность кода и данных, и, позволяя эффективно использовать много токенов в левой части производственного правила, состояние не ограничивается представлением одним атомом: мы можем использовать кортеж атомов, и это позволяет (не рекурсивные) подпрограммы. Это очень полезно для гольфа. Единственное, чего на самом деле не хватает, так это макросов и возможность отладки.

Для массивов я использую функцию сопряжения, которая может быть реализована в ГМ. Пустой массив представлен$0$и результат предварительного $x$ массив $A$ является $(2A+1)2^x$, Существует одна подпрограмма для сопряжения: вызывается подпрограмма, Pи она добавляет значение eto b. Есть две подпрограммы, которые нужно разомкнуть: nотсоединение bот eи b; и tunpairs dк eи d. Это позволило мне сохранить немного перетасовываемых данных между переменными, что важно: одна операция «перемещение»

a, b = b, 0

расширяется как минимум до 17 байтов:

S+a->S+b
S+0a->T

где Sтекущее состояние и Tследующее состояние. Неразрушающий «копия» еще дороже, потому что это должно быть сделано как «шаг» от aк bи вспомогательной tmp, с последующим «хода» от tmpспины к a.

затемнение

Я связывал различные переменные друг с другом и исключил около 60 штатов в процессе игры в гольф, и многие из них в любом случае не имели особо значимых имен, но для полной игры в гольф я написал минимизатор, поэтому имена теперь совершенно не поддаются расшифровке. Удачи, обратный инжиниринг это! Вот минимизатор (в CJam), который делает несколько предположений о коде, но может быть адаптирован для минимизации других программ Alchemist:

e# Obfuscate / minimise Alchemist program

e# Tokenise
qN%[SNS]e_*S%

e# Get token frequencies for substitution purposes, special-casing the I/O ones
_["+" "0" "2" "->" "_" N "In_n" "n" "Out_tmp2" "tmp2"]-
$e`$W%1f=

e# Empirically we want a two-char input for n and a one-char one for tmp2
["In_n" "Out_tmp2" "n" "tmp2"]\+
["In_NN" "Out_a" "NN"] "abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ"1/:A+ A2m*:e_"NN"a-+
1$,<

er
_s,p

Пари / ГП , 118 байт

Прямой перевод ответа Питера Тейлора на CJam .

n->(s(k)=subst(a,x,x^k));(z()=(a^2+s(2))/2);a=O(1);for(i=0,n,a=1+x*(a*z()+(s(3)-a^3)/3));a=z();Pol(a+x*(s(2)-z()))\x^n

Попробуйте онлайн!